.
¡Genial!, eres un pura sangre. Otro cualquiera habría desistido.
Tú tienes un empeño, que ya lo hubiera querido yo para mí.
Hay que tener genes para atacar el vaivén de cifras que tú has meneado.
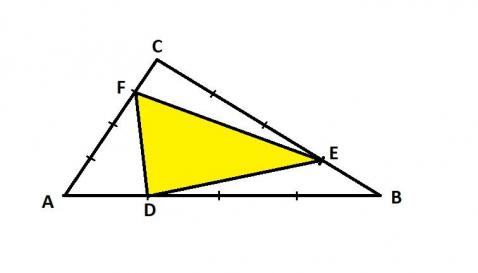
Ocurre en este problema como en el de los dos triángulos: las medidas, los cálculos, no son el camino hacia su solución.
Es necesario hacer reflexiones, más que sobre los números que manejes en sí, sobre lo que ellos significan.
Aquí no importa si la velocidad de los trenes es 100, 1, o un millón de kms. Lo que importa es lo que significan esas cantidades, Qué son unas y qué son otras.
Has observado que el tren B visita cada ciudad cuando recorre 200 km.
También has observado que el tren A visita cada ciudad cuando recorre 141'4213562... km = 100xRaízCuad (2)
Es decir, el tren B visita las ciudades en múltiplos de 200 y el tren A las visita en múltiplos de 100xRaízCuad (2)
Por tanto, para que ambos trenes coincidan en alguna de sus visitas, debes responder a estas preguntas:
¿Es posible que un múltiplo ENTERO de 200 coincida con un múltiplo ENTERO de 100xRaízCuad (2)?. Digo ENTERO, porque si no fuese ENTERO entonces los trenes estarían en algún punto interior de su trayecto y no podrían coincidir (Uno va por la diagonal y el otro por los lados).
Y si esa coincidencia se produjese, ¿estarían los dos trenes en la misma ciudad?
Y para ello vienen a cuento mis comentarios sobre la variación continua del tiempo y sobre los decimales. Aquí los decimales han de tenerse en cuenta hasta el infinito, de lo contrario, sólo tendrás aproximaciones de las cantidades que se manejen, y las aproximaciones tienen una propiedad, ¡que son exactas!, cosa que no ocurre con todas las cantidades teóricas.
Por ejemplo, el número pi no puede ser alcanzado con múltiplos ENTEROS de 1, porque requeriría 3'1415926... de estos múltiplos.
Tampoco con múltiplos ENTEROS de 0'5, porque requeriría 6'283185307... múltiplos.
Ni tampoco con múltiplos ENTEROS de 0'1 porque requeriría 31'415926535... de estos múltiplos
Y así sucesivamente.
El caso es que siempre estaría comprendido entre dos de estos múltiplos, pero nunca sería igual a uno de ellos.
Por ejemplo, el número pi está comprendido entre el tercer y cuarto múltiplo del 1.
Entre el sexto y séptimo múltiplos de 0'5.
Entre el 31 y el 32 múltiplos de 0'1,
¡Pero nunca coincide con uno de ellos!, porque ellos son EXACTOS (son aproximaciones) y el número pi NO es una aproximación, y si lo es, solo se debería a que previamente HA SIDO MUTILADO, recortado y privado de sus infinitos decimales.
Te lo dejo ahí, el resto es cuestión de reflexión y observación.
Saludos
PD. Considero importante hacer esta aclaración:
La dificultad de este problema no está en que 100xRaízCuad (2) sea decimal. Ni en que las variaciones del tiempo también lo sean. De hecho hay decimales, como por ejemplo 0'5, que son iguales a múltiplos ENTEROS de otros decimales: 0'5 = 5x (0'1).
Tampoco está la cuestión en que la variación sea axacta o que tenga infinitas cifras decimales, por ejemplo 5x200 = 9000x (0'1111111111111.....)
Realmente reside en un aspecto muy peliagudo sobre lo que es el número RaízCuad (2). En casi todos los libros de primer curso de la ESO viene explicado.
Y por último, ¿qué pasaría si Antonio fuese en el tren A al encuentro de su novia Beatriz que viene a encontrarse con él en el tren B?
.
... (ver texto completo)